Lower bounds in distributed computing are very helpful. Obviously, they prevent you from wasting time trying to do impossible things :-). Even more importantly, understanding them well often helps in finding ways to focus on what is optimally possible or ways to circumvent them by altering the assumptions or the problem formulation.

Its either easy or impossible – Salvador Dali

In this post we discuss a classic impossibility result:

DLS88 - Theorem 4.4: It is impossible to solve Agreement under partial synchrony against a Byzantine adversary if $f \geq n/3$.

As described in an earlier post on partial synchrony, either we have a GST event at an unknown time (or we have an unknown $\Delta$). Thus, the time to decide cannot depend on GST occurring (or on knowing $\Delta$).

Seeking a contradiction, let us assume there is a protocol that claims to solve Byzantine Agreement with $f \geq n/3$ Byzantine parties. Divide the $n$ processors into three sets: $A$, $B$, and $C$ each with at least one party and at most $f$ parties in each set. We consider the following three worlds and explain the worlds from the view of $A$, $B$, and $C$. In all three worlds, we will assume that all messages between $A \longleftrightarrow B$ and $B \longleftrightarrow C$ arrive immediately; but all messages between $A$ and $C$ are delayed by the adversary.

For the proof approach we introduce two simple (but powerful) techniques. These two techniques are used in many other proofs so it’s worthwhile to get to know them.

The first is indistinguishability, this is where some parties can not tell between two (or more) potential worlds. Their distribution of views looks exactly the same so they must decide the same way in both worlds. This leads to the following initial proof approach: imagine that there were two worlds: world 1 and world 2. Imagine that in world 1 the honest must decide 1 and in world 2 the honest must decide 0. If there was some honest party for which world 1 and world 2 are indistinguishable then we would drive a contradiction. Unfortunately we cannot use such a simple argument for this lower bound.

The second technique is hybridization, this is where we build intermediate worlds between the two contradicting worlds and use a chain of indistinguishability arguments to create a series of statements that leads to the final contradiction.

Here we go, lets define worlds 1, 2, and 3:

World 1:

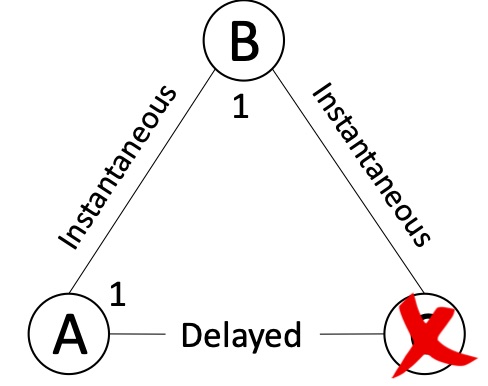
In World 1 parties in $A$ and $B$ start with the value 1. Parties in $C$ have crashed. Since $C$ is at most $f$ participants, the parties in $A$ and $B$ must eventually decide. For agreement to hold, all the parties in $A$ and $B$ will output 1. From the perspective of $A$ (and also $B$), they cannot distinguish between a crashed (or Byzantine) $C$ vs. an honest $C$ whose messages are delayed.

World 2:

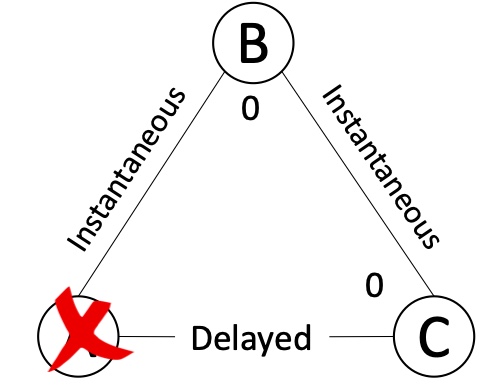
World 2 will be a world similar to world 1 where the roles of $A$ and $C$ are interchanged. The parties in $B$ and $C$ start with the value 0. Parties in $A$ have crashed. Again, $C$ cannot distinguish between a crashed $A$ vs. an honest $A$ whose messages are delayed. So all the parties in $C$ and $B$ will output 0.

World 3:

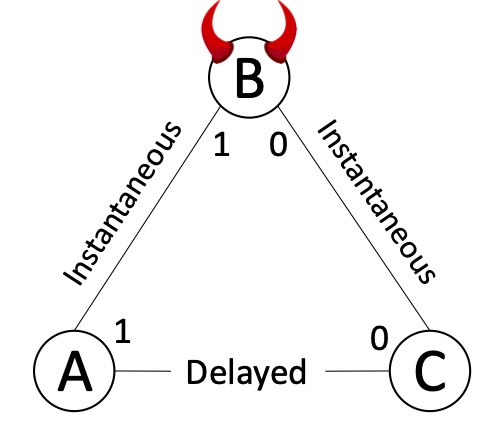
World 3 will be a hybrid world where the view of $A$ in this world will be indistinguishable to the view of $A$ in world 1 and the view of $C$ in this world will be indistinguishable to the view of $C$ to world 2. $A$ will start with value 1 and $C$ will start with value 0. The adversary will use its Byzantine power to corrupt $B$ to perform a split-brain attack and make $A$ and $C$ each believe that they are in their respective worlds. $B$ will equivocate and act as if its starting value is 1 when communicating with $A$ and as if its 0 when communicating with $C$. If the adversary delays messages between $A$ and $C$ for longer than the time it takes for $A$ and $C$ to decide in their respective worlds, then by an indistinguishability argument, $A$ will commit to 1 and $C$ will commit to 0 (recall the time to decide cannot depend on GST or $\Delta$). This violates the agreement property.

Some important observations:

  1. The impossibility holds even if the adversary is static, i.e., we fix the set $B$ that the adversary corrupts before starting the execution.

  2. The impossibility holds even if there is a trusted setup phase, for example if the parties have a PKI setup.

  3. The impossibility above importantly assumes (i) a Byzantine adversary for $B$, and (ii) messages between $A$ and $C$ can be delayed sufficiently. Even if one of these two conditions do not hold, we can tolerate $f \geq n/3$. If we only have crash faults, then Paxos and many other protocols can tolerate a minority corruption. If messages are guaranteed to arrive within a fixed known time bound (i.e., assuming synchrony), then we can tolerate a minority corruption (see for example here, here, and here).

  4. For agreement to hold, it is essential that if one party decides on a value, all other parties decide on the same value. Under partial synchrony, since parties are not even guaranteed to be able to communicate with each other before they decide, they always ensure that a majority of honest parties ``agree’’ to a value before deciding (otherwise two minorities can commit to different values). Among $3f+1$ parties, $f$ can be Byzantine; thus $f+1$ honest parties form a majority among the remaining $2f+1$. Hence, partially synchronous protocols typically communicate with $2f+1$ (out of $3f+1$) parties before deciding: $f+1$ honest majority + (up to) $f$ Byzantine. On the other hand, under synchrony even a single honest party can inform all other honest parties. Thus, synchronous parties typically communicate with $f+1$ out of $2f+1$ parties.

  5. A similar lower bound holds for crash (or omission) failures if $n \leq 2f$ in the partial synchrony model. See this post on this and the CAP theorem for more.

  6. This lower bound holds for Broadcast (aka Reliable Broadcast) in partial synchrony, not just for Agreement.

Please leave comments on Twitter