In a previous post, we show that State Machine Replication for any $f<n$ failures is possible in the synchronous model when the adversary can only cause parties to crash. In this post, we show that omission failures are more challenging. Implementing SMR requires at most $f<n/2$ omission failures, even in synchrony.
Theorem: It is impossible to implement State Machine Replication with two replicas for two clients and an adversary that can cause omission failures to one replica (and any number of clients) even in a lock-step model.
As in our previous lower bounds, we assume an implementation of a Write Once Register State Machine that obtains Termination, Agreement, Validity and Correctness and reach a contradiction. For the contradiction, we define three worlds and use an indistinguishability argument. In each world, there are two clients called client $1$ and client $2$ and two servers called server $1$ and server $2$.
World A:
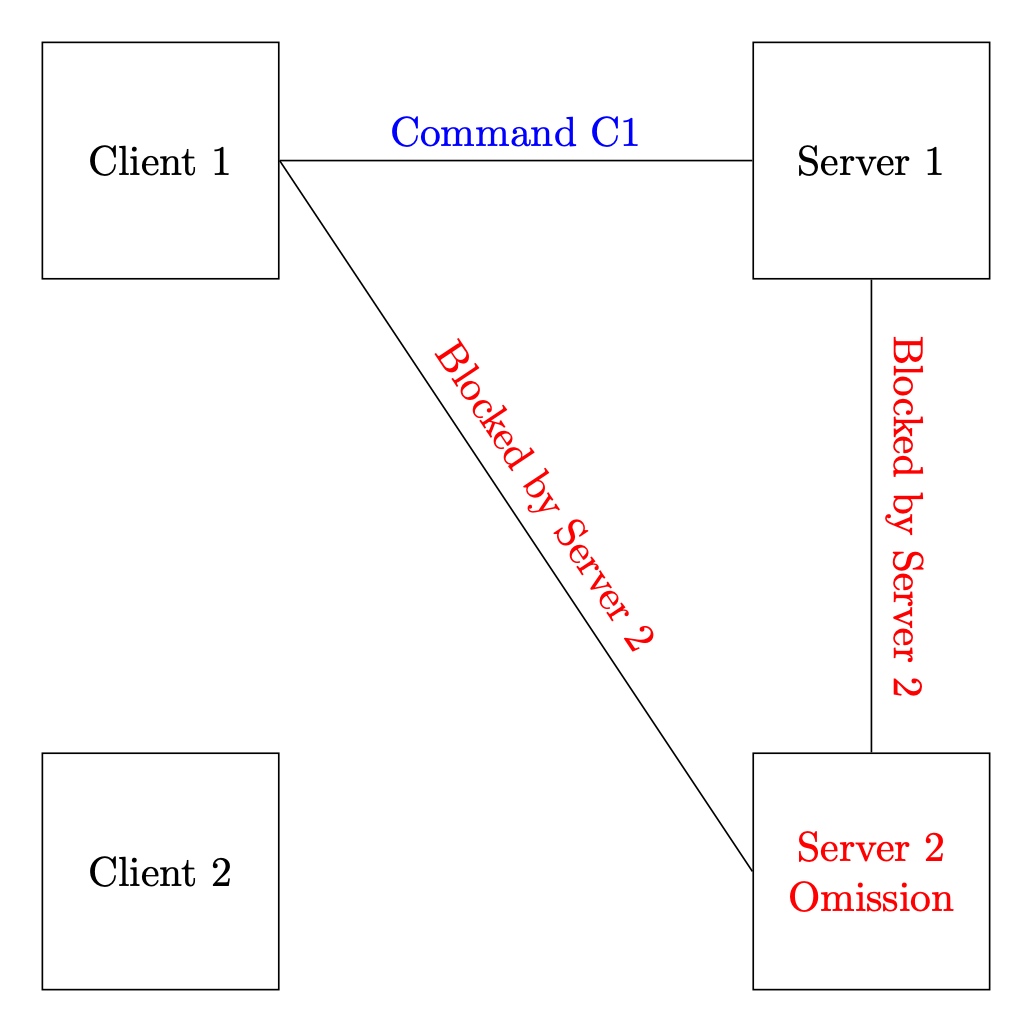
In this world, client $1$ wants to send command $C1$, and the adversary blocks all communication to and from server $2$ (server $2$ is omission faulty). Since the protocol obtains Termination and client $1$ is non-faulty, then it must get a response. Since the protocol obtains Validity and Correctness, it must notify client $1$ that command $C1$ is the only committed command.
World B:
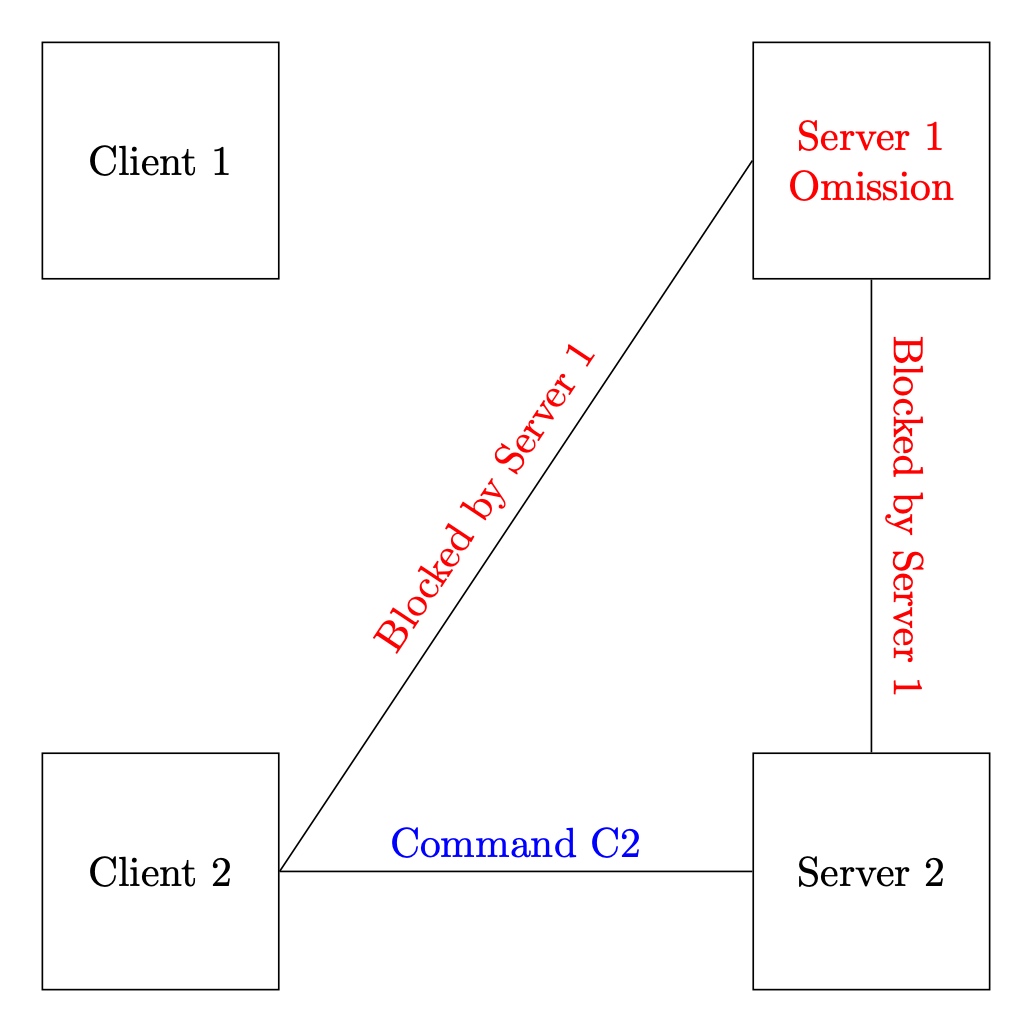
In this world, client $2$ wants to send command $C2$, and the adversary blocks all communication to and from server $1$ (server $1$ is omission faulty). Since the protocol obtains Termination and client $2$ is non-faulty, then it must get a response. Since the protocol obtains Validity and Correctness, it must notify client $2$ that command $C2$ is the only committed command.
World C:
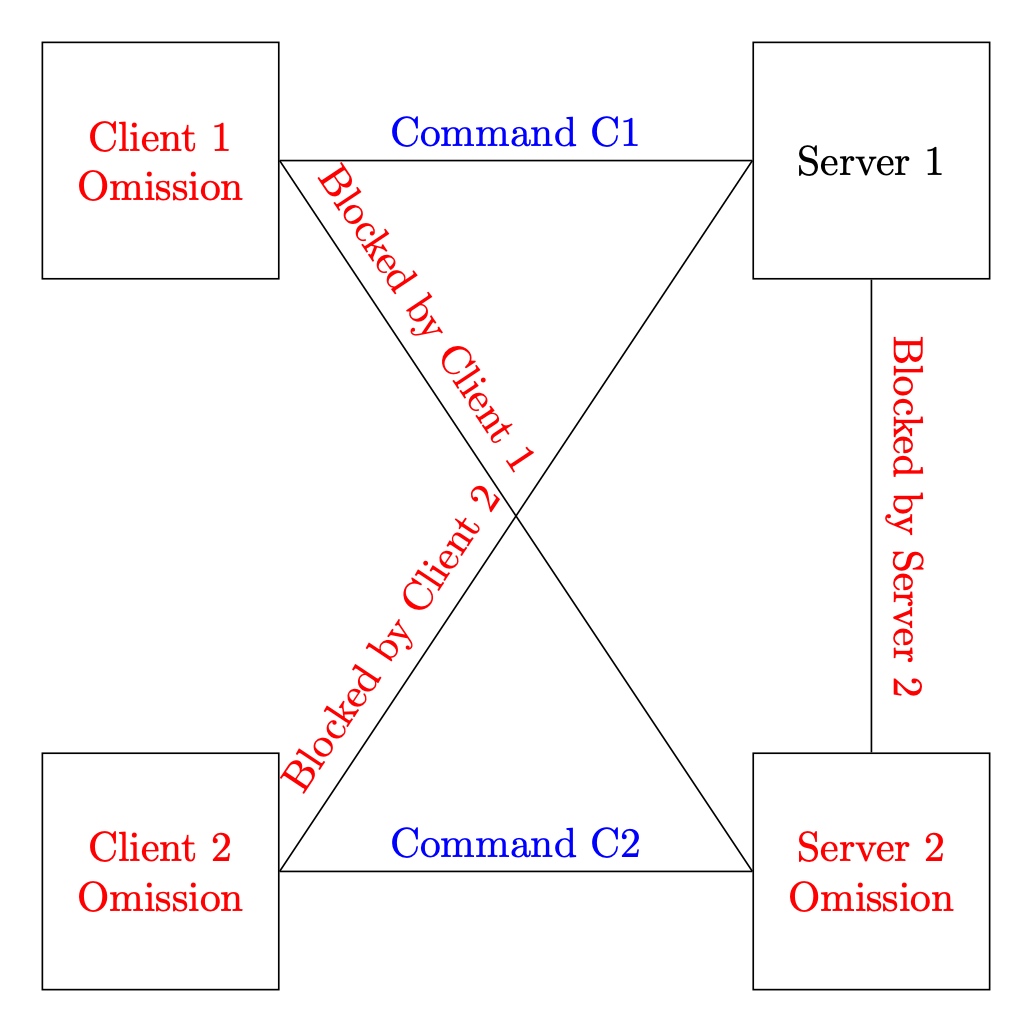
In this world, client $1$ wants to send command $C1$, and client $2$ wants to send command $C2$. The adversary causes both clients to fail by omission as follows: it blocks all communication between client $1$ and server $2$ and all communication between client $2$ and server $1$. Finally, without loss of generality, the adversary also causes server 2 to have omission failures by blocking all communication between server $1$ and server $2$.
Observe that the view of server 1 in world A and world C is indistinguishable. Since in worlds A and C, client $1$ only communicates with server $1$, it also has indistinguishable views.
Similarly, the view of server 2 in world B and world C is indistinguishable. Since in worlds B and C, client $2$ only communicates with server $2$, it also has indistinguishable views.
So in world C, the two clients will see conflicting states and this is a violation of safety. In particular a violation of the agreement property that clients should have.
Notes:
- The proof heavily uses the fact that the clients are prone to omission failures. If clients can just crash (or are non-faulty) then the clients can implement SMR using the replicas as relays.
- This lower bound can be generalized to $n$ replicas and $f$ omission failures for any $n\leq 2f$.
- Since it just requires omission faults, this lower bound holds even if there is a setup and a PKI (or any other cryptographic assumptions and setups).
- This post was updated in November 2021 to stress that the lower bound requires at least two clients. In fact, the state machine we need is a simple two-client write-once register.
- Nancy Lynch’s book has a variant of this lower bound for atomic objects in asynchrony. See Theorem 17.6 in her book.
- This was later extended by Gilbert and Lynch to partial synchrony and connected to Browers conjecture. We cover this in our post on the CAP theorem.
Please leave comments on Twitter