In the previous post, we discussed progress in authenticated synchronous consensus protocols. In this post, we will discuss one of the recent protocols Sync HotStuff, which is a simple and practical Byzantine Fault Tolerant SMR protocol to tolerate $f < n/2$ faults.
We first present one of the key ideas of Sync HotStuff. Later, we briefly discuss some of the other results in the paper. In order to be practical, the main goal of Sync HotStuff is to allow replicas to commit with as low latency as possible. Sync HotStuff works in the steady-state-and-view-change paradigm. In the steady-state, it achieves a latency of $2\Delta$ time, where $\Delta$ is the bounded-message delay. Here is how we achieve it. For simplicity, we describe the key idea for agreement on a single value in the steady-state. All messages are digitally signed.
-
Propose. The leader proposes a command cmd.
-
Vote. On receiving the first valid proposal from the leader, a replica will broadcast a vote for it. When a replica votes, it also forwards the leader proposal to all other replicas.
-
Commit. If a replica does not receive a proposal for a conflicting command cmd’ $\neq$ cmd within $2\Delta$ time after voting, commit cmd.
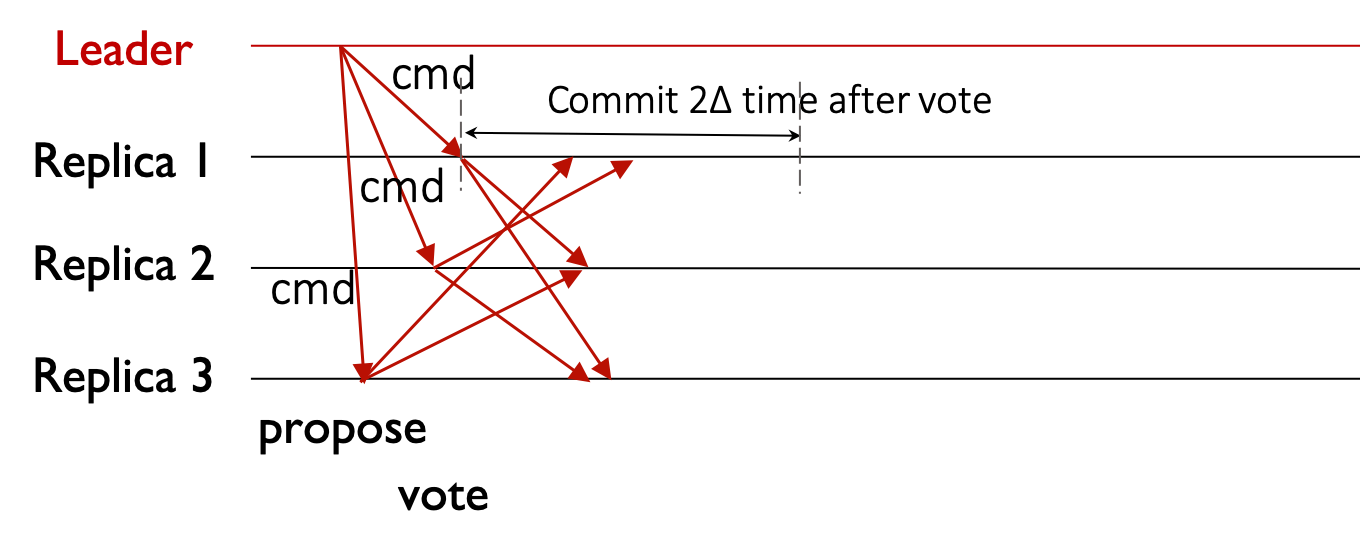
A pictorial illustration for a three replica execution is presented in the figure. The key question is why does a $2\Delta$ time after vote suffice to commit? How does it ensure safety?
The $2\Delta$ waiting time suffices for two invariants to be satisfied if the committing replica receives no conflicting command: (i) cmd will be certified, i.e., it will be voted for by all honest replicas, and (ii) no conflicting command will be certified.
Suppose replica 1 is committing cmd at time $t$. Let us understand the sequence of events from its point of view, pictorially represented in the picture below.

Since replica 1 committed at time $t$, it must have voted at time $t - 2\Delta$. This vote also acts as a re-proposal, and hence all honest replicas receive the proposal by time $t-\Delta$. If no honest replica has received a conflicting command at $t-\Delta$, then the honest replica will vote for cmd, and cmd will be certified. If an honest replica receives a conflicting command cmd’ after $t-\Delta$, then cmd’ will not be voted for (a replica only votes for the first valid proposal). If it received cmd’ before $t-\Delta$, it would indeed vote for cmd’. But this vote will arrive at replica 1 before time $t$, causing replica 1 not to commit. Thus, a $2\Delta$ wait after a vote suffices to commit.
The above description only explains the scenario where the leader is honest, and there are no conflicting proposals. Otherwise, we will need a mechanism to identify conflicting proposals or lack of progress and perform a view change. We refer readers to the paper for the details on the view change procedure.
The paper also presents a few other results. One of the disadvantages of synchrony is that a single failed message can result in safety loss. Sync HotStuff can tolerate a weaker synchrony model proposed by Guo et al.. This allows the protocol to work even if the synchrony assumption is violated at a small fraction of honest nodes at any time. Moreover, Sync HotStuff is optimistically responsive, i.e., it can commit in less than $\Delta$ time when $>3n/4$ nodes are honest. Finally, the empirical evaluation shows that its throughput is comparable to the best known partially synchronous protocols.
This protocol is a joint work with Ittai, Dahlia and Ted. It is in S&P 2020. Read more about it here.
Acknowledgment. We would like to thank Ittai for helpful feedback on this post.