Proof of Work (PoW) Blockchains implement a form of State Machine Replication (SMR). Unlike classical SMR protocols, they are open, i.e., anyone can join the system, and the system incentivizes participants, called miners, to follow the protocol. Therefore, unlike classical SMR protocols, reasoning about blockchain security relies not only on bounding the number of malicious participants. One should crucially ask whether miners are indeed incentivized to follow the prescribed protocol. This is the topic of this post.
To make things concrete, we’ll consider Nakamoto’s Bitcoin protocol. Ling already provided background and an analysis of security against malicious adversaries. For our analysis, we’ll describe the system as a game played among miners.
The Game
The players are the miners who generate blocks. The game proceeds in rounds, where in each round one miner generates a block and any miner can publish blocks it has generated. Publication is done with synchronous broadcast, so all miners receive messages published in the previous round.
This is of course a simplification, e.g., it ignores the slow variation in the total mining power in the system and forks that happen accidentally, which are rare but still occur. Nevertheless, this model is sufficient as a first order approximation of the system.
The prescribed protocol is for each miner to extend the longest chain, or the one it heard of first, in case of a fork where two branches have the same length.
Each player in the game strives to maximize her revenue – this is her utility function. Specifically, we consider an infinite-horizon game, that is, the revenue of a miner is her average ratio of blocks in the main chain as the game length tends to infinity. This represents the reward in terms of cryptocurrency granted to miners for each block they generate. Note that blocks that end up outside the main chain (pruned) do not count towards the miner’s revenue.
Important observation
The ratio of blocks on the main chain is indeed an approximation of the revenue in real terms.
Suppose the total mining power in the system is static with blocks generated in 10 minute intervals and the attack starts right after a difficulty adjustment. Consider a strategy that results in a consistent rate of blocks that are pruned, say 20% of the blocks generated by all miners. So blocks are still generated every 10 minutes in the system, but only 80% are in the main chain, making its block interval 12.5 minutes instead of 10. The Bitcoin blockchain updates its difficulty once every 2016 blocks, which is going to take longer than usual ($12.5 \times 2016$ minutes instead of $10 \times 2016$ minutes).
Once the difficulty adjustment occurs, the difficulty is reduced such that the main chain block interval becomes 10 minutes again. This means the total block generation rate in the system is now higher, with an interval of only 8 minutes.
So a miner with a ratio $\alpha$ of the total mining power and a ratio $\alpha’ > \alpha$ of the blocks on the main chain is going to get a revenue proportional to $\alpha’$ per hour (instead of proportional to $\alpha$ per hour).
Selfish Mining Algorithm
Selfish Mining (SM) is a strategic mining algorithm that demonstrates that the prescribed protocol is not an equilibrium for minority miners in general. Let’s see the mechanics of Selfish Mining, and then discuss when and why it works.
Initially, the selfish miner tries to extend the longest chain, as she’s supposed to. However, once she generated a block, she keeps it secret rather than publishing it, and then tries to extend it further, forming a secret branch.

Meanwhile, the other miners extend the public chain, which will eventually become longer (with probability 1) since they are the majority. The selfish miner continues to extend her secret branch until the public chain is one step behind. Then she publishes her secret chain.
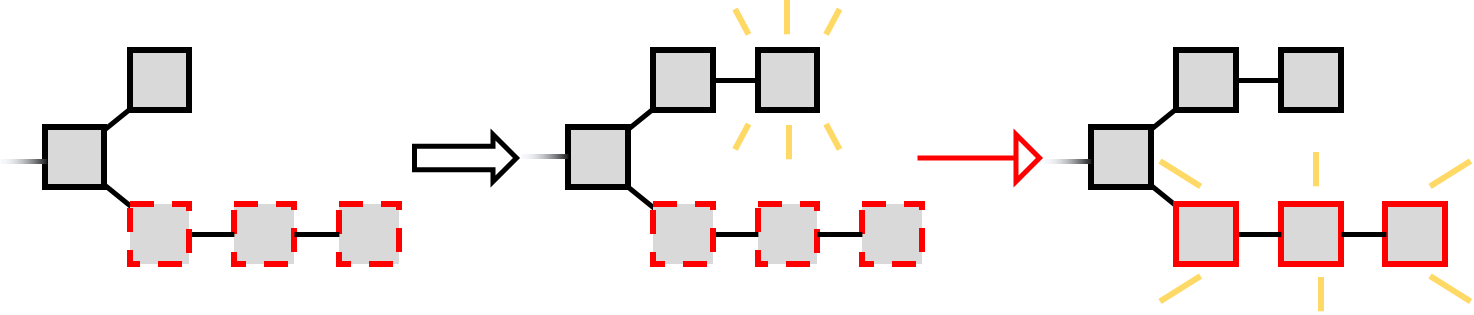
Since the secret chain is longer, the other parties consider it the main chain, so now everyone is following the selfish miner’s blocks. The blocks generated by the other miners are thus pruned - ignored and confer no reward to their creators.
But there is a caveat to this strategy - when first forming her secret chain, the selfish miner takes a risk. If she generated the first secret block and then another miner generated a block, she cannot publish her secret block and have the longest chain; instead, it will be a race between two branches of length one.
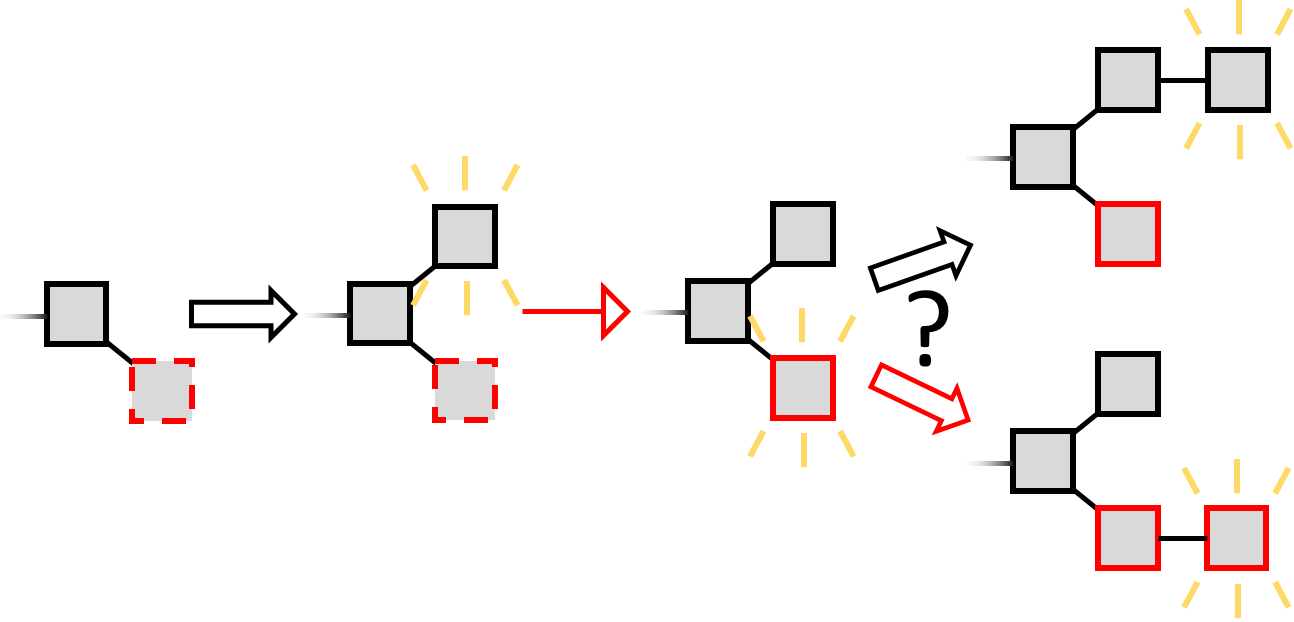
The selfish miner will try to extend her own branch, and for simplicity let us assume that all other miners will try to extend the other branch. If she wins she publishes her block, which is the longest chain, and the attack restarts at the end of this longest chain. If the other miners win, the selfish miner is at a disadvantage (shorter branch). In this case she gives up the attack attempt and starts again. She gains no revenue from her pruned formerly-secret block.
Selfish Mining Analysis
At first glance it might seem that the attack would not work - the minority miner is going to lose more races that she wins. However, a careful analysis shows this is not the case in general. The game can be naturally described as a Markov Chain. By accounting for each block from the selfish miner and from the other miners, we can calculate the ratio of the selfish miner’s blocks and her revenue out of all blocks as a function of her size.
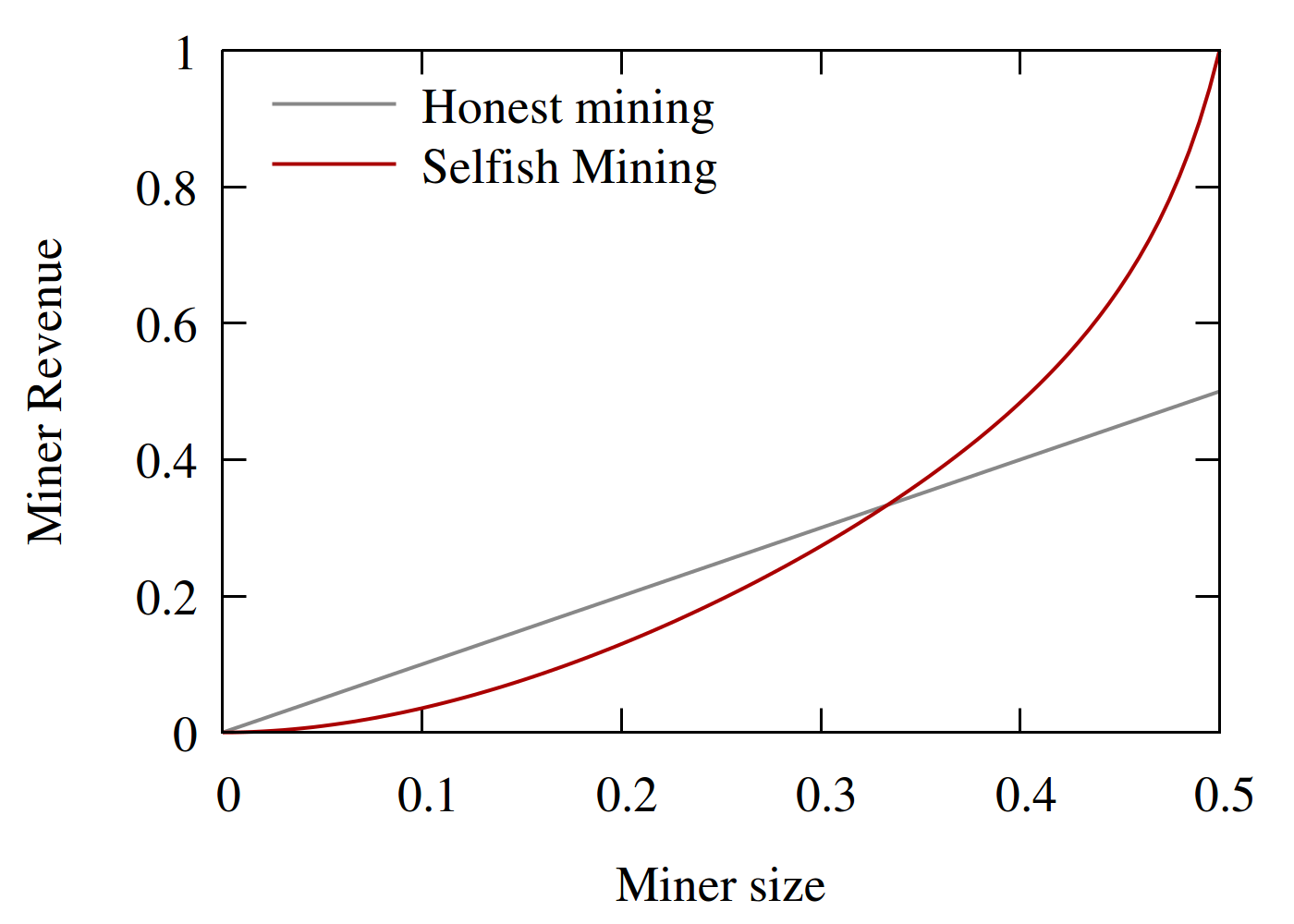
We see that a selfish miner larger than 1/3 of the mining power would increase her revenue by deviating from the prescribed protocol and performing Selfish Mining.
Conclusion
The analysis has demonstrated that Selfish Mining outperforms honest mining when the selfish miner is larger than 1/3, but this is an optimistic bound. For a deeper dive that including weaker models and a patch to strengthen the protocol, take a look at the Selfish Mining paper in Financial Crypto, 2013 and in the Communications of the ACM, 2018.
Subsequent work, including recent results, use Markov Decision Processes to provide thresholds for miners under which there is no better strategy than honest mining.
Acknowledgment. Thanks to Ittai Abraham for helpful feedback on this post.
Please leave comments on Twitter.