Synchronous consensus protocols tolerating Byzantine failures depend on the maximum network delay $\Delta$ for their safety and progress. The delay, $\Delta$ is usually much larger than actual network delay $\delta$ since $\Delta$ is a pessimistic value. While synchronous protocols tolerating more than one-third will have executions with at least a $\Delta$ latency, recent synchronous protocols such as Sync HotStuff have been trying to reduce the reliance on $\Delta$ as much as possible.
Can we commit faster than a $\Delta$ time for some executions? Indeed. By using the notion of optimistic responsiveness! The work Thunderella introduced this notion allowing synchronous protocols to commit in $O(\delta)$ time when certain optimistic conditions are met. In their protocol, the optimistic conditions require an honest leader and $>3n/4$ honest replicas. They introduce a “slow-path–fast-path” paradigm with two distinct commit paths: (i) an optimistic fast commit path with a commit latency of $O(\delta)$, and (ii) a slow synchronous commit path with a commit latency of $O(\Delta)$.
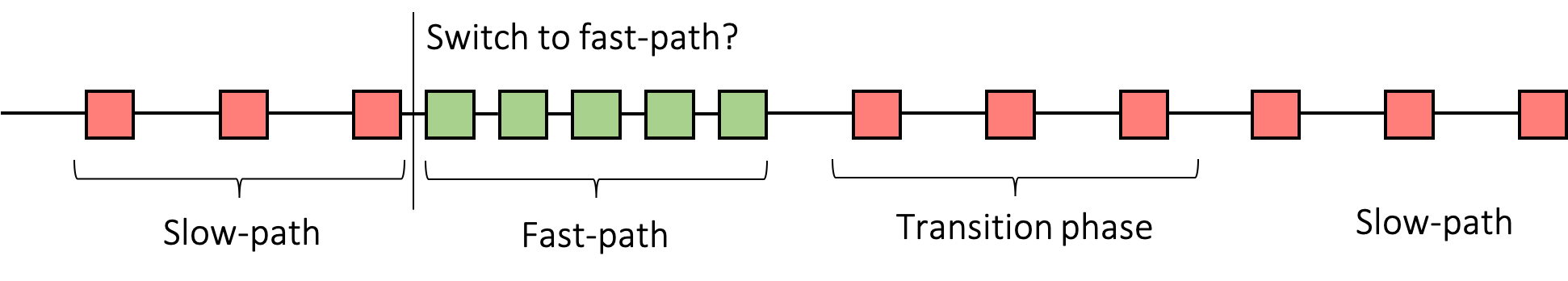
When optimistic conditions are met, the replicas make an explicit switch to the fast path. If the fast path does not make progress, they switch back to the slow path through an intermediate transition phase. However, unfortunately, there is no easy way to determine if the optimistic conditions are met. If the replicas cautiously move to the fast path, they will have missed opportunities for committing early for some transactions. Otherwise, it may be the case that optimistic conditions did not hold requiring us to switch back to the slow path through the transition phase. A slow slow-path and a slow transition phase only worsens the problem. Can we do better?
Can we always obtain optimal latency independent of the conditions?
We answer this question in our recent work on the optimality of optimistic responsiveness. In this post, we will first explain what optimality means for the latency of an optimistically responsive synchronous protocol, and then provide protocols with such an optimal latency.
Lower bound on the latency of optimistically responsive protocols
Informally, our lower bound result says the following:
There does not exist a Byzantine Broadcast protocol that can tolerate $f \geq n/3$ faults and when all messages between
non-faulty parties arrive instantaneously, achieves the following simultaneously under an honest designated sender:
(i) (optimistic commit) a commit latency of $O(\delta)$ in the presence of $\max(1, n − 2f)$ faults,
(ii) (synchronous commit) a commit latency of < $2\Delta − O(\delta)$ in the presence of $f$ faults.
Informally, the lower bound says that the sum of latencies of these two commit rules should be at least $2\Delta$. This bound on latency holds when the following conditions are met:
- The total number of faults tolerated $f \geq n/3$: otherwise, we can always commit responsively by using a partially synchronous protocol.
- The designated sender is honest: otherwise, a Byzantine sender may not send a value and no replica will be able to commit optimistically.
- The optimistic commit rule tolerates at least one fault: if this condition does not hold, we show an upper bound that circumvents this lower bound.
- All messages between non-faulty parties arrive instantaneously: this condition attempts to provide the best possible network conditions to a protocol. Hence, if a protocol does not have a good latency when this condition holds, it is unlikely that the protocol will commit faster when the communication is not instantaneous.
Optimal Optimistic Responsiveness
The latency constraints described in the lower bound can indeed be obtained: our protocol commits responsively with a commit latency of $2\delta$ when the leader and $>3n/4$ replicas are honest, and commits with a latency of $2\Delta$ otherwise. The protocol works in the steady-state-and-view-change paradigm with a single leader until an equivocation or no progress is detected. A view-change protocol is executed to elect a new leader and ensure safety when the current leader fails to make progress. Our core consensus protocol in the steady-state is extremely simple, and can be described as follows:
- Propose. The leader proposes a command cmd.
- Vote. On receiving the first valid proposal from the leader, a replica broadcasts a vote for cmd and forwards the leader proposal to all other replicas.
- Commit.
(i) Responsive Commit. If a replica receives $\lfloor 3n/4 \rfloor + 1$ votes for cmd and detects no “bad events”, commit cmd immediately. Notify commit to all replicas.
(ii) Synchronous Commit. If a replica detects no “bad events” within $2\Delta$ time after voting, commit cmd.
This protocol is similar to the non-responsive Sync HotStuff protocol. The only difference is the presence of an additional responsive commit rule. In the protocol, a “bad event” implies a potential leader misbehavior such as detecting an equivocation or obtaining a blame certificate to overthrow the leader. Thus, a replica commits responsively when it receives a responsive quorum of votes, i.e., $\lfloor 3n/4 \rfloor + 1$ for cmd (responsive certificate) and has not detected bad events. Similarly, a replica r synchronously commits cmd if it does not detect a bad event within $2\Delta$ time after voting. In this case, replica r receives at least a synchronous quorum of $f+1$ votes for cmd (synchronous certificate). We note that a responsive quorum for cmd and a synchronous quorum for cmd’ does not necessarily intersect at an honest replica. Yet, our protocol maintains safety at all times when the corruption threshold is $< n/2$.
Here’s an intuitive reasoning for the safety of the steady state protocol at a given height. Suppose honest replicas r and r’ commit cmd and cmd’ respectively at a given height. We require cmd = cmd’. Replicas r and r’ can commit using different commit rules:
- Both replicas commit responsively: this is not possible due to a quorum intersection argument (will be explained in a later post).
- Both replicas commit synchronously: this not possible due to an argument presented in Sync HotStuff.
- Replica r commits responsively whereas replica r’ commits synchronously: this is not possible due to the following reason.
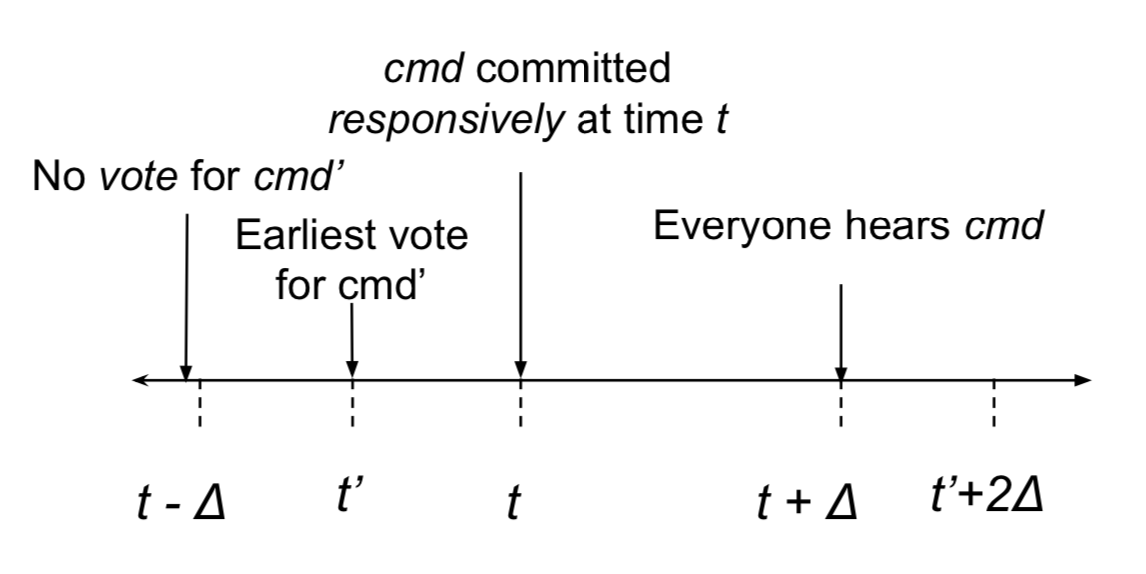
Suppose an honest replica r commits cmd responsively at time t. This implies (i) no honest replica has voted for a conflicting command cmd’ before time $t-\Delta$, and (ii) all honest replicas will hear a vote for cmd by time $t+\Delta$. The earliest an honest replica r’ could have voted for cmd’ is at time $t’$ such that $t-\Delta \le t’ \le t$. Since, replica $r’$ learns cmd by time $t+\Delta \le t’ +2\Delta$, it would not commit cmd’ synchronously. Additionally, since a responsive quorum requires $\lfloor 3n/4 \rfloor + 1$ votes, two responsive quorums intersect at least one honest replica. Thus, no conflicting command could get committed responsively.
The above explanation suffices to argue why two conflicting commands cannot be committed at the same log position. Within a state machine replication (SMR) setting, replicas keep voting and committing new commands by extending on previously proposed commands thus forming a linear chain of commands. As we just saw, there could exist a responsive certificate and a synchronous certificate for conflicting commands. As a result, there could be conflicting chains extending from conflicting responsive and synchronous certificates. We resolve this conflict by proposing a novel chain ranking rule that ranks responsive certificates higher than synchronous certificates We refer the readers to our paper for more details on chain ranking and the complete protocol specification.
Remarks. In the paper, we present two additional protocols:
- an optimal optimistic responsive protocol with only $\Delta$ synchronous latency. This protocol requires all $n$ replicas to be honest; thus we circumvent the ‘optimistic rule should tolerate at least one fault’ constraint.
- a protocol that allows the view-change protocol to be responsive too. This was not obtained in either of the other protocols.
This is a joint work with Ittai and Ling. Read more about it here.
Please leave comments on Twitter.