Encrypted Blockchain Databases (Part II)

In this second part of the series on Encrypted Blockchain Databases, we are going to describe three schemes to store dynamic encrypted multi-maps (EMMs) on blockchains, each of which achieves different tradeoffs between query, add and delete efficiency.

A List-Based Scheme (LSX)

Recall that a multi-map is a collection of multiple label/value tuples. In this construction, we store the values associated with each label into separate logical linked-lists on the blockchain. However, to guarantee confidentiality, we encrypt each value concatenated with the previous address, before adding it to the right linked-list. Precisely, given a tuple $(v_1, \dots, v_n)$ to be added to label $l$, for each $i \in [1, n]$, we add $Enc_K(v_i || r_{i-1})$ to the blockchain. For the first value, $r_{i-1}$ is the address of the current head of the linked-list of $l$. To achieve dynamism, we use lazy deletion, i.e., all the added and deleted values are marked as added (+) or deleted (-) and deletion is only performed at query time by removing the values marked as deleted from the output. Refer to Figure 1 for an illustration of LSX – for clarity, we omit the encryption of the values and addresses from the figure.

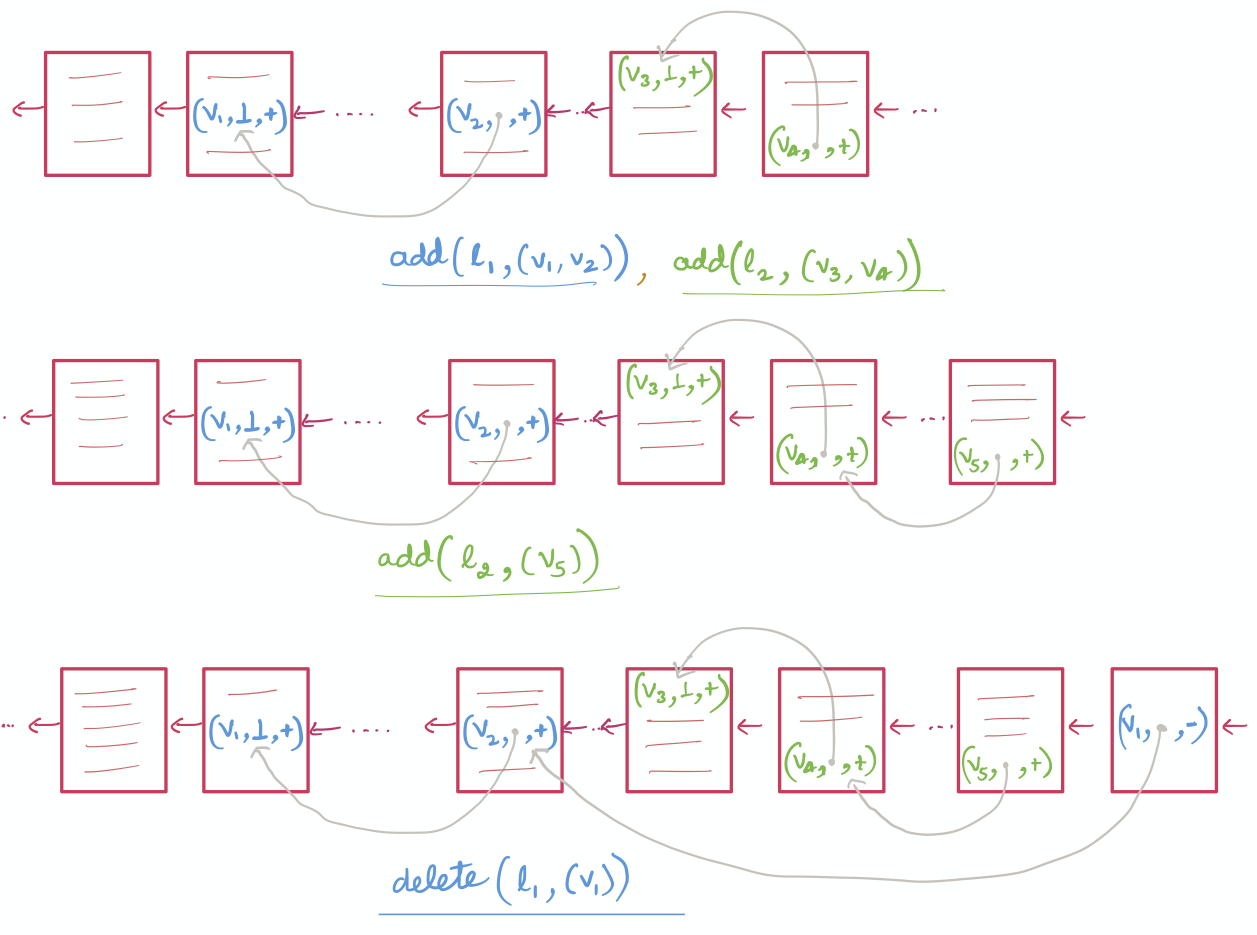
Efficiency. It is easy to see that LSX has optimal add and delete time complexity: for each operation, we only write as many values as the size of the tuple. However, its query complexity is linear in the number of updates. In particular, on every query, we read all the values that were ever added or deleted. If all update operations are additions, then this scheme has optimal query complexity, but if most updates are deletions, then the scheme incurs non-trivial query overhead. There is one more shortcoming of this scheme: both add and delete operations take a linear number of write rounds (in the size of the tuple) between the user and the blockchain. This is due to the fact that a value $v_i$ cannot be written until the address of $v_{i-1}$ has been computed and thus each value has to be written in a separate write round.

Counting the number of write rounds is important because blockchain writes take much longer than blockchain reads, due to mining and stabilization. It, therefore, becomes important to parallelize writes as much as possible. We call this metric the stabilization complexity, because the time it takes to write depends on the time it takes for a transaction to become stable – for example for Bitcoin, write time can be up to 60 minutes (a block has to be at least 6 levels deep in the chain to become immutable).

Next, we describe a tree-based scheme which improves the stabilization complexity from linear to logarithmic.

A Tree-Based Scheme (TRX)

In this scheme, we modify the way the values are organized with the goal of reducing the number of addresses needed before storing a value. Given a tuple to add/delete, we super-impose a complete binary tree instead of super-imposing a linked list on the blockchain. This allows us to parallelize the insertions of all the values that are at the same depth of the tree. Furthermore, we also link the roots of the trees constructed across multiple add/delete operations. Notice that this simple structural change reduces the stabilization complexity from linear to logarithmic.

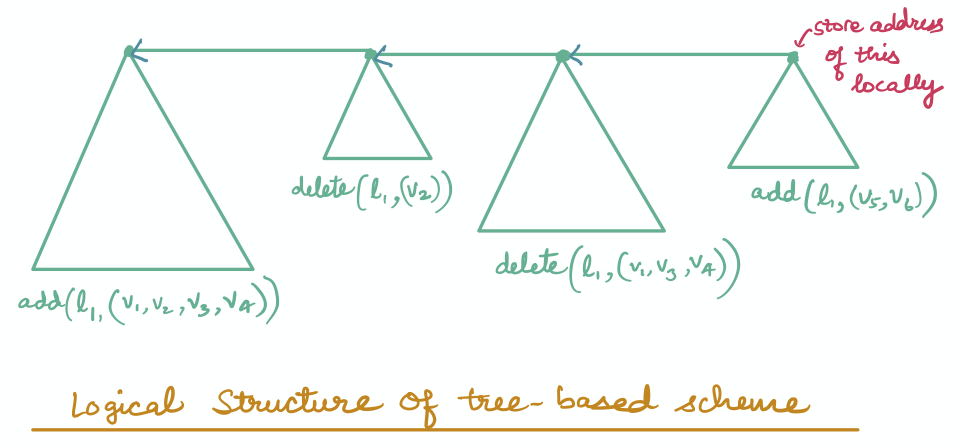
Since both the schemes described above have a query complexity linear in the number of values ever added/deleted – which can be terrible when most updates are delete operations – we now describe a scheme that improves the query complexity to be optimal but at the cost of making deletes a little expensive.

A Patch-Based Scheme (PAX)

Notice that the query complexity of LSX is not optimal because we do not know the values that are deleted while traversing the linked list¹, and hence we end up reading all the values, irrespective of whether they are deleted or not. To fix this, we super-impose additional data structures, called patches, on top of the linked-list. Patches are address pairs that will allow the query algorithm to skip deleted values. For example, suppose we have the following linked-list:

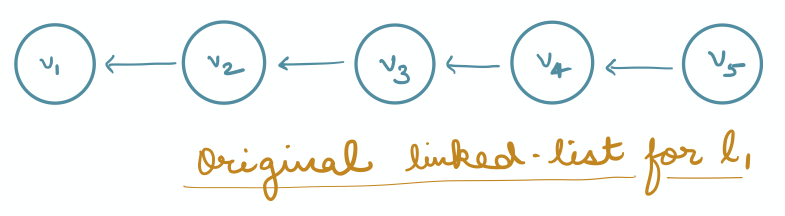
On deleting $v_2$, we create a patch $(addr(v_3) \rightarrow addr(v_1))$, and on deleting $v_4$, we create another patch $(addr(v_5) \rightarrow addr(v_3))$. For now, we do not worry about where and how the patches are stored. But given these patches, the query algorithm can easily skip over the deleted values $v_2$ and $v_4$: from $v_5$, it will use the second patch to jump to $v_3$, and from $v_3$, it will use the first patch to jump to $v_1$.

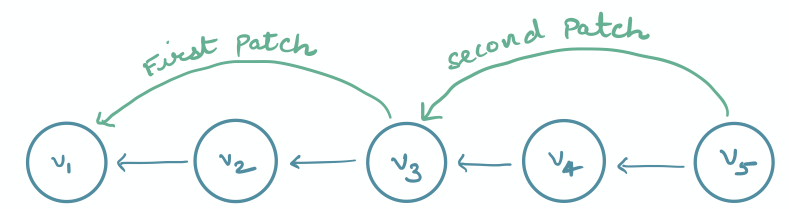
Now suppose $v_3$ also gets deleted. In this case, we create a new patch $(addr(v_5) \rightarrow addr(v_1))$ which can help the query algorithm to jump over all the values $v_2$, $v_3$ and $v_4$.

There are two issues with this:

1. There are two patches from $v_5$: one that goes to $v_3$ and one that goes to $v_1$. For a query to correctly skip over the deleted values, it should use $(v_5 \rightarrow v_1)$ instead of $(v_5 \rightarrow v_3)$.

2. The number of patches is equal to the number of deleted values, which means searching for a patch is as expensive as employing lazy deletion.

To address this, we need to make sure that we clean up (or remove) old patches. Precisely, we should remove both $(v_5 \rightarrow v_3)$ and $(v_3 \rightarrow v_1)$ when $v_3$ is deleted. Deletion of $(v_5 \rightarrow v_3)$ guarantees correctness while deletion of $(v_3 \rightarrow v_1)$ guarantees efficiency since the number of patches left are at most the number of un-deleted values.

Patch data structure. Since the number of patches can be significant, they cannot be stored locally and have to be stored on the blockchain as well. We can organise patches in either a linked-list or a tree. Whatever we decide, let’s call the structure the patch structure. Notice that, irrespective of how we organise the patch structure on the blockchain, the requirement to delete patches from it introduces a chicken and egg problem: deletion of multi-map values from the linked-list requires deletion of patches from the patch structure. So should we patch the patch structure?

We use another technique called copy on write to solve this dilemma. At a high level, the technique makes a copy of the “node”, and makes modifications to the copy instead of modifying the original node. We explain it with an example. Suppose that we represent the patch structure as a linked-list. Further, suppose that there are 100 patches $P_1 \ldots P_{100}$ in the patch structure.

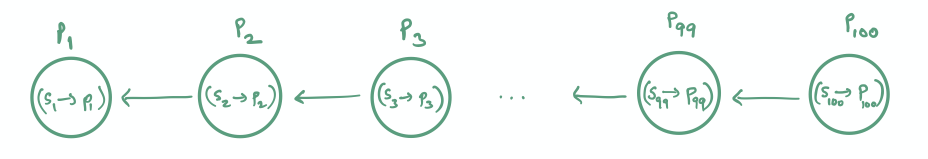
To delete $P_2$, we need to make $P_3$ point to $P_1$. Since $P_3$ is stored on the blockchain, however, it cannot be changed to point to $P_1$. We therefore create a copy $P_3’$ of $P_3$, such that it stores the same patch data as $P_3$ but points to $P_1$. However, this requires $P_4$ to point to the copy $P_3’$, which cannot be done since it is also stored on the blockchain. Therefore a copy $P_4’$ of $P_4$ is created. This process propagates up to the head of the linked-list and every node from $P_3$ to $P_{100}$ is replaced with its copy.

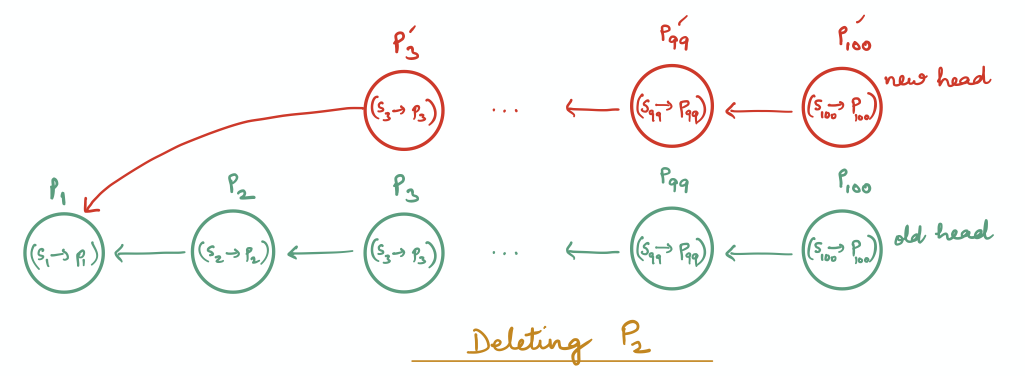
Clearly, this is very expensive: deleting a patch that is very deep in the patch structure’s linked-list triggers all the subsequent patches to be re-written. Therefore, we instead represent the patch structure as a balanced binary tree, in which case a patch deletion only triggers the creation of as many patches as the height of the tree.

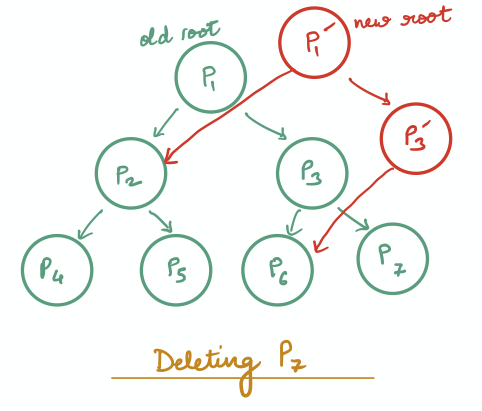
Efficiency. Let $|MM[l]|$ be the number of values currently associated with label $l$ in the multi-map. In other words, $|MM[l]|$ represents the number of un-deleted values for $l$. We will not argue it here, but it’s not hard to see that the number of patches in the patch structure is at most $|MM[l]|$. Since the query algorithm can now jump over the deleted values using the patches, and searching for a patch is inexpensive, the time complexity for query is $O(|MM[l]|)$, which is optimal. The complexity of an add operation is the same as before and hence is also optimal. The delete complexity is $O(|v|\log |MM[l]|)$, where $|v|$ is the number of values being deleted. This is because for every value that is deleted, a new patch is inserted in the patch tree and/or an old patch is deleted which takes $(\log |MM[l]|)$ time.

Stabilization complexity. Since the add operations add values as linked lists (same as in LSX), the stabilization complexity of an add is $O(|v|)$. However, the stabilization complexity of delete is $O(\log |MM[l]|)$ because all the modifications done at the same level of the patch tree can be made in parallel.

Conclusion

We discussed how to integrate end-to-end encryption in blockchain databases and, more precisely, ways to store end-to-end encrypted multi-maps on blockchains. Since multi-maps are expressive enough to represent key-value stores, this provides a way to store key-value stores on blockchains. We discussed three EMM constructions that achieve different tradeoffs between query, add, and delete efficiencies. There are however some open questions that would be interesting to answer.

We showed that, while TRX has optimal add/delete time complexity, TRX has poor query complexity. PAX, on the other hand, achieves good query complexity but has poor stabilization add/delete complexity. This motivates the following natural question:

Can we design a scheme that achieves the best of both worlds?

We also show in our paper that both LSX and TRX can use packing, which allows multiple tuple values to be stored in a single transaction. For blockchains that allow large transactions, packing can lead to large performance improvements. Unfortunately, our PAX construction does not support packing, so a natural question is

Can we incorporate packing in PAX?

Please leave comments on Twitter.