In this post, we highlight the connection between Broadcast and Agreement in the synchronous model.
Broadcast and Agreement: How can you implement one from the other?
We defined Agreement and Broadcast in a previous post, here is a recap:
Agreement
A set of $n$ nodes where each node $i$ has some input $v_i$. A protocol that solves Agreement must have the following properties.
(agreement): no two honest nodes decide on different values.
(validity): if all honest nodes have the same input value $v$ then $v$ must be the decision value.
(termination): all honest nodes must eventually decide on a value in $V$ and terminate.
Broadcast
Here we assume a designated node, often called the leader (or dealer) that has some input $v$. A protocol that solves Broadcast must have the following properties.
(agreement): no two honest nodes decide on different values.
(validity): if the leader is honest then $v$ must be the decision value.
(termination): all honest nodes must eventually decide on a value in $V$ and terminate.
Broadcast from Agreement
Suppose you have access to a black-box Agreement protocol $A$ and you want to implement Broadcast:
- In the first round, the leader sends its input $v$ to all.
- In the second round, each party starts the Agreement protocol $A$ with the input being the value it received by the end of round 1 from the leader (or some default non-value if no value is heard).
- The output of the Broadcast is the output of $A$.
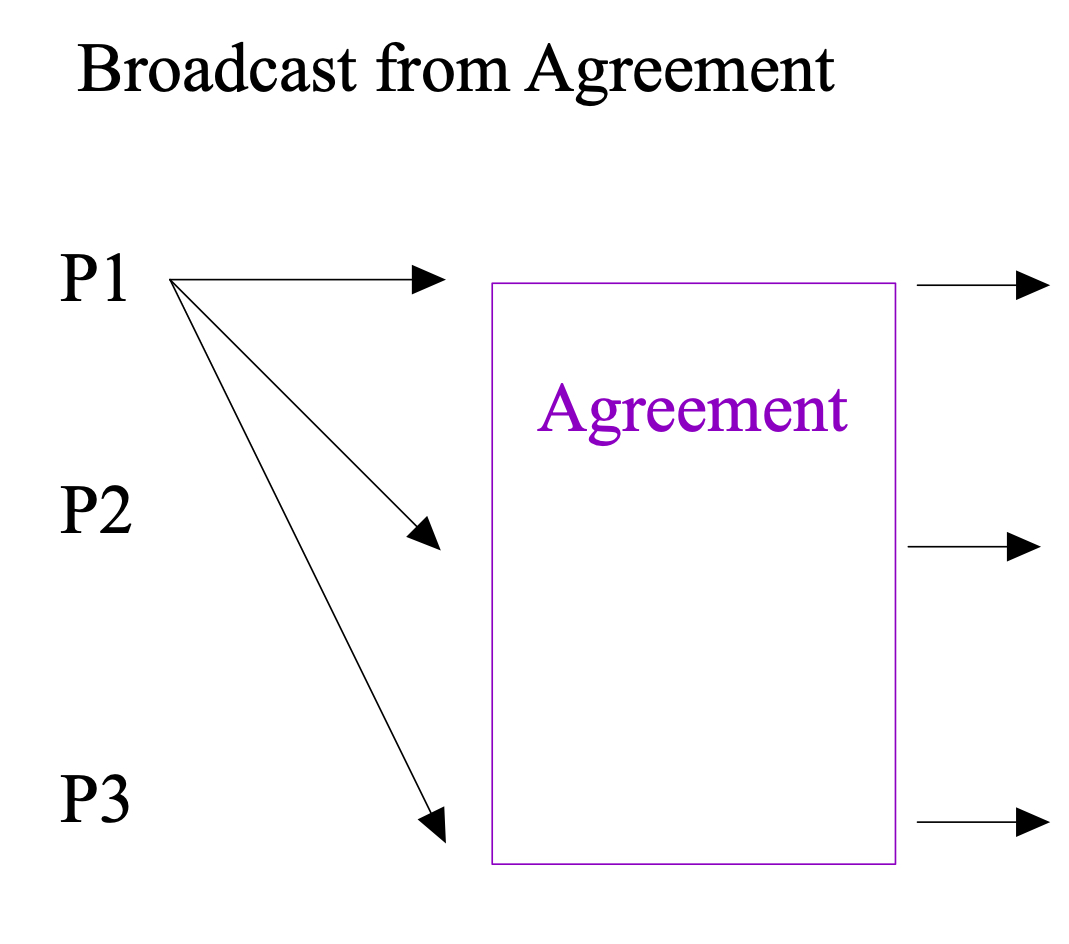
Claim: The protocol above implements Broadcast.
Proof: Termination is immediate from the termination of $A$. Validity follows from the validity of $A$: if the leader is honest, then all honest will start $A$ with the leader value $v$ and hence will decide $v$. Agreement immediately from the agreement property of $A$.
Discussion: Note that all we needed for the reduction is to add $n$ messages and one additional round. This means that any lower bound for Broadcast about $x$ messages and/or $y$ rounds, implies a matching lower bound of at least $x-n$ messages and/or $y-1$ rounds for agreement!
Agreement from Broadcast
Here we need to assume $f<n/2$. Suppose you have black-box access to a Broadcast protocol and you want to implement Agreement:
- Each party $i$ Broadcasts its input value $v_i$.
- Once all the broadcasts complete, output the majority value (break ties deterministically and choose a default value if all values are empty).
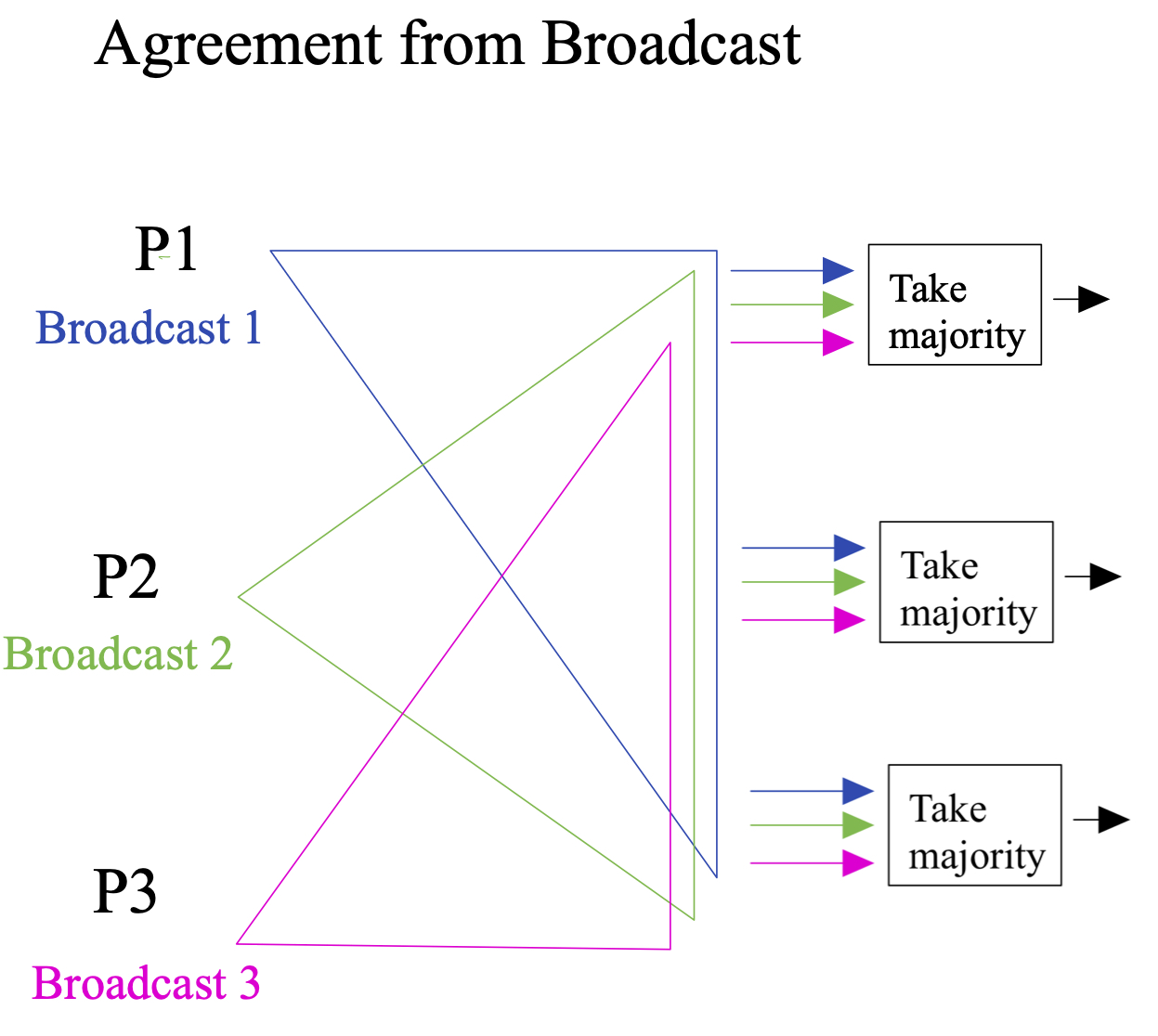
Claim: The protocol above implements Agreement for $f<n/2$.
Proof: Termination follows from the termination of $B$, note that we need all broadcasts to terminate (this can affect the costs if the termination is a random variable). Validity follows from the validity of $B$ and the fact that $f<n/2$: if all honest have the same input $v$, then $v$ will be the majority value since the honest are a strict majority. Agreement follows from the agreement property of $B$ and the deterministic nature of the reduction.
Discussion: For this reduction we needed to run $n$ instances of Broadcast to get one Agreement. This means that any lower bound for Agreement about $x$ messages and/or $y$ rounds, implies a matching lower bound of at least $x/n$ messages and/or $y$ rounds for agreement.
Scratch your Brains!
Exercise 1: Can you extend the above reductions to the asynchronous model?
Exercise 2: A different definition for consensus is that of interactive consistency (IC) first defined by Lamport, Shostak, and Pease. In this definition, each party $i$ has an input $v_i$. Each party $j$ commits an n-tuple $(v_1^{j}, v^j_2, \ldots, v^j_n)$. The definition requires the following properties to hold:
(agreement): For any two honest parties $P_j$ and $P_k$, $v^j_i = v^k_i, \forall i \in [n]$.
(validity): If party $P_i$ is honest, for every honest party $P_j$, $v^j_i = v_i$.
(termination): All honest nodes must eventually decide on a set of values and terminate.
Can you perform a similar reduction to obtain IC using (i) Agreement and (ii) Broadcast, and vice-versa.
Please discuss/comment/ask on Twitter.