Many modern BFT protocols share a common structural pattern. PBFT uses preprepare and prepare. Tendermint uses prevote and precommit. CasperFFG and Simplex use notarization and finalization. HotStuff uses a QC on top of another QC.

Notice the pattern? Each of these protocols begins with a proposal followed by two voting rounds. This raises a natural question:

Is one round of proposing followed by two rounds of voting actually necessary?

This recurring structure suggests that the two voting rounds are not an accident but a fundamental requirement. Indeed, any BFT protocol that is resilient to $f$ malicious parties and has at most $5f-2$ servers must have a round of proposal and two rounds of voting even in the good-case.

All the protocols above have optimal resilience of $n=3f+1$ for $f \geq 2$ so fall into that category of $n\le 5f-2$.

The decision latency is the time it takes for all honest parties to decide after $GST$.

It is known that the worst-case decision latency is $O(f)$ rounds. The good-case latency of a broadcast protocol is the decision latency when the leader is honest and $GST=0$. The main result we cover in this post is:

Theorem [ANRZ21]: Any protocol that solves Byzantine Broadcast in partial synchrony for $n\leq 5f-2$ that tolerates $f$ Byzantine failures must have a good-case latency of at least $3$ rounds.

Proof

The proof is by contradiction. Assume there is a protocol that has a good-case decision latency of 2 rounds and show that it must fail.

For any $f\geq 2$, partition the $n=5f-2$ parties into the leader and 5 sets $A,B,C,D,E$ with sizes:

$|A|, |E|=f$ and $|B|,|C|,|D|=f-1$.

(If $n$ is smaller, then choose these sets to be smaller but non-empty)

We consider three executions: a mixed world $M$, a corrupt world $\hat{D}$, and a validity world $V$.

World $M$ (mixed)

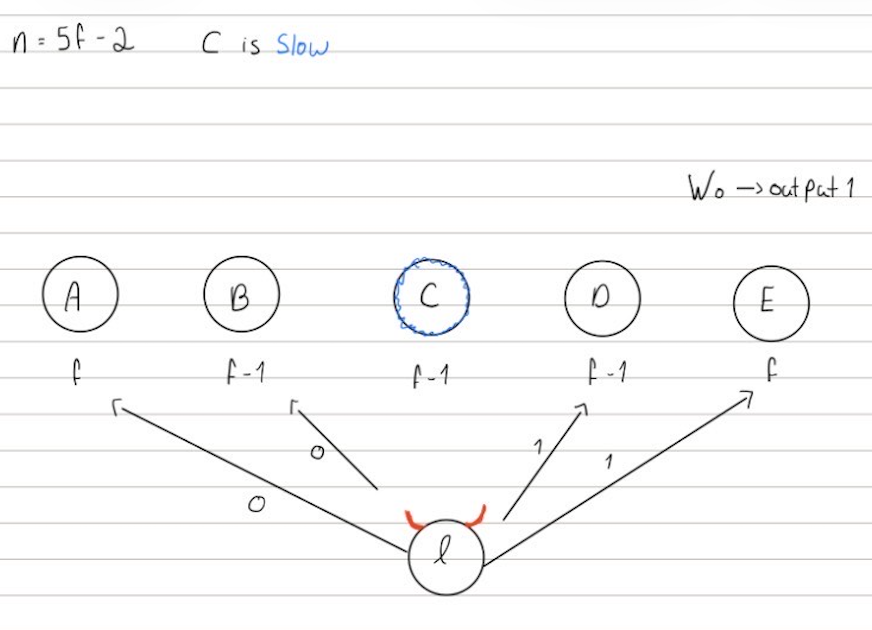
In the mixed world, the leader and parties in $C$ are Byzantine. Also, $GST = 0$. The leader sends $0$ to $A,B$ and 1 to $D,E$.

In these executions assume without loss of generality that the protocol decides 1 with probability at least one half.

World $\hat{D}$ (corrupt)

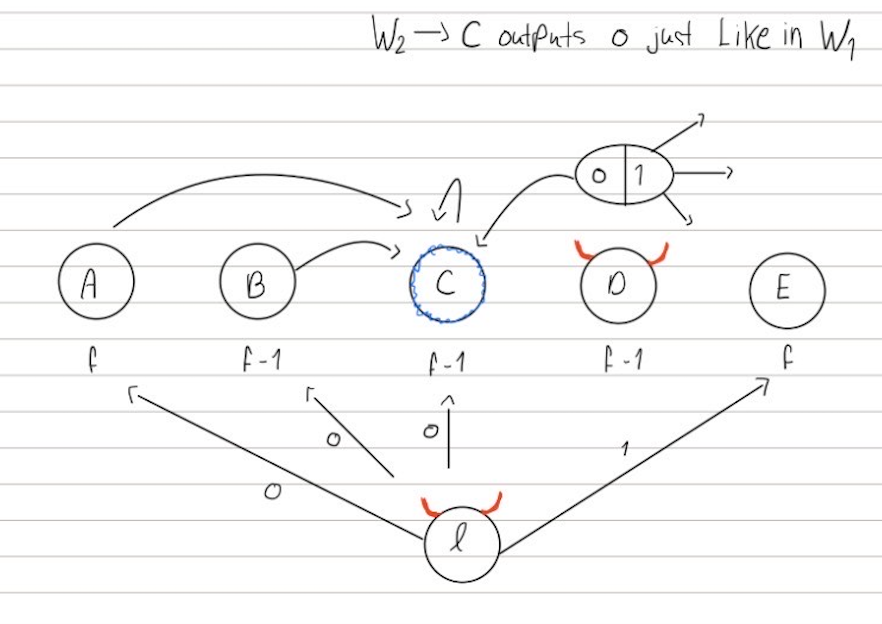
In this corrupt world, the leader and parties in $D$ are Byzantine. $GST$ appears after $A$ and $E$ decide. The leader sends $0$ to $A,B,C$ and 1 to $E$. The parties in $D$ act as if they received 1 when talking to $A$, $B$, and $E$, and they send round one voting messages to $C$ as if they received $0$ from the leader.

Observe that $B$ and $E$ cannot distinguish between worlds $M$ and $\hat{D}$. Thus, they must decide 1 (at least half the time). Consequently, all honest parties (including set $C$) must decide 1.

World $V$ (validity)

In this validity world, $GST = 0$, the parties in set $E$ are Byzantine. The leader is honest and sends $0$ to all. The set $C$ hears $0$ from $A,B,D$ and decides 0 in two rounds (one round of voting). Deciding 0 is necessary for validity to hold in this world.

The contradiction

To make the argument explicit, we group the indistinguishability claims. First, $B$ and $E$ cannot distinguish worlds $M$ and $\hat{D}$, which forces them to decide 1 in both. Second, $C$ cannot distinguish worlds $\hat{D}$ and $V$ up to the decision point. Combined, these two indistinguishability links yield the contradiction.

Now we can reach a contradiction by showing that in world $\hat{D}$ where the decision is 1, the set $C$ will see the same messages as in world $V$ and hence decide 0 after two rounds for a safety violation (at least half the time).

A concrete example

Applying this to PBFT, assume an (incorrect) PBFT that decides after seeing a certificate of $2/3$ of preprepare messages (instead of $2/3$ of prepare messages), what would go wrong?

In PBFT, in world $M$ the first leader would not reach $2/3$ of preprepares, so let’s assume the second leader is honest and will cause all honest to decide 1. But that means that all honest will also decide 1 in world $\hat{D}$. In world $V$ the parties in $C$ will see more than $2/3$ preprepare for 0 and hence early decide on 0. That implies that in world $\hat{D}$ the parties in $C$ will decide 0 while the other honest parties decide 1.

Notes

  • We used world $\hat{D}$ where $D$ is malicious. This choice depends on the decision in world $M$ being 1. In the symmetrical case where the decision is 0, we would use world $\hat{B}$ where $B$ is malicious: it plays as if it has $0$ to $A,D,E$, and it sends round one of voting messages to $C$ as if it has 1.

  • When $n\geq 5f-1$ it is possible to have a good-case latency of just $2\delta$. For example, see this post or this one.

  • In particular, when $f=1$ we have $3f+1=5f-1=4$ and hence can have a good-case of two rounds in that setting.

  • This previous post provides an overview of the complete categorization of latency lower bound for the good-case in both synchrony and partial synchrony.

  • In this post we discuss the good-case latency for synchronous protocols.

  • The proof in [ANRZ21] also takes care of protocols in which other parties send round 0 messages. Intuitively, this should not matter as they know nothing about the input. Indeed, adding this is a rather straightforward extension, and we removed it from this post for clarity of the main argument.

Acknowledgments

Many thanks to our co-authors Ling Ren and Zhuolun Xiang. Thank you, Samuel Laferriere for inspiring us to write this post.

Please leave comments on X