In this post we explore adversary failure models that are in between crash and omission:

  1. Send Omissions (SO): the adversary can corrupt a party and decide to block any message that the party sends. The corrupted party is not aware that it is corrupted or that the message it wanted to send was blocked.
  2. Receive Omissions (RO): the adversary can corrupt a party and decide to block any message that the party receives. The corrupted party is not aware that it is corrupted or that the message it was supposed to receive was blocked.
  3. Send or Receive Omissions (SRO): the adversary can corrupt a party with either send omissions or receive omissions but not both.

Can you guess in which models state machine replication is possible for any $f<n$ and for which ones we can’t do better than $f<n/2$? The answer is that in models where you can detect failures you can get $f<n$.

Primary Backup for Send Omissions for $n=2$ and $f=1$

The solution is similar to the primary backup solution for crash failures with the following two changes:

To deal with send omissions from the primary to the client: the backup also sends the response back to the client.

To deal with send omissions from the primary to the backup: The primary sends a heartbeat every $\Lambda$ time. If the backup does not hear a heartbeat in $\Delta+\Lambda$ period it sends a message to the Primary (and everyone) saying that the primary is faulty. The Primary then halts itself and the Backup becomes the new primary. The Client may need to re-transmit its request to the new primary. Note that we can unequivocally detect the Primary has failures.

Primary Backup for Receive Omissions for $n=2$ and $f=1$

The solution is again similar to the primary backup solution for crash failures with the following two changes:

To deal with receive omissions of the primary from the client: the client sends to both the primary and the backup and the backup forwards the request to the primary. The primary executes commands only once via unique identifiers.

To deal with receive omissions of the primary from the backup: The backup sends a heartbeat every $\Lambda$ timer. If the primary does not hear a heartbeat in $\Delta+\Lambda$ period it sends a message to all saying it crashed. The Primary then halts itself and the Backup becomes the new primary. The Client may need to re-transmit its request to the new primary. Note that we can unequivocally detect the Primary has failures.

Primary Backup for Send or Receive Omissions is impossible $n=2$ and $f=1$

Recall that here the adversary can corrupt at most one server with either send of receive omission (but not both) and can also corrupt any number of clients (again with either send or receive omissions).

In the figures below, arrow-less lines represent bidirectional communication, while lines with an arrow represent communication only in the direction of the arrow (other direction is blocked).

The main idea of the lower bound is that when communication from Server 2 to Server 1 fails we cannot detect if the problem is Server 1 having receive omissions or Server 2 having send omissions. We use the fact that clients can also have omissions to make sure that clients also cannot detect the problem.

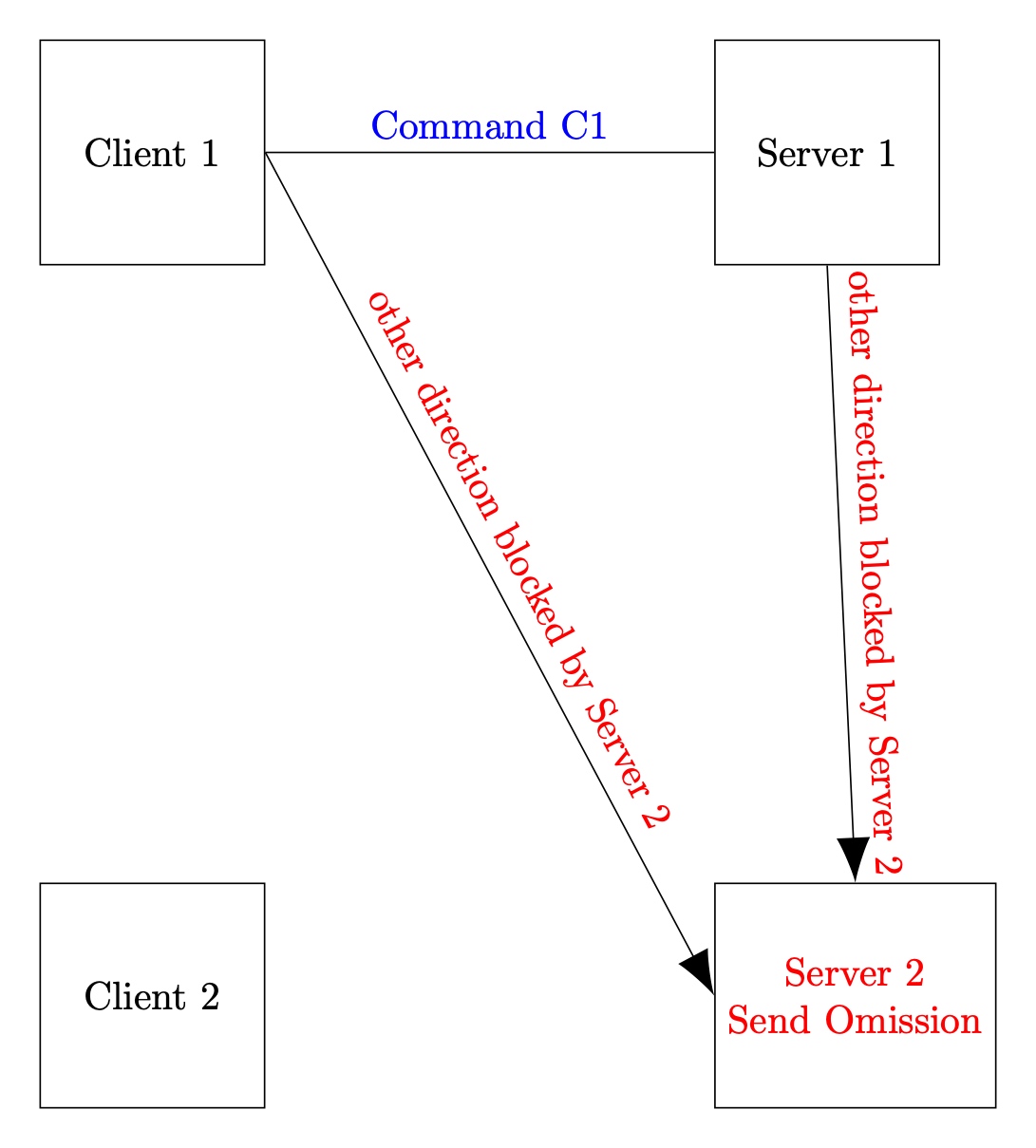
World A: Server 1 has Receive Omission failures

Server 1 cannot receive any message. Nevertheless, Client 2 and Server 2 must complete the request. Note that Server 1 learns nothing of this request.

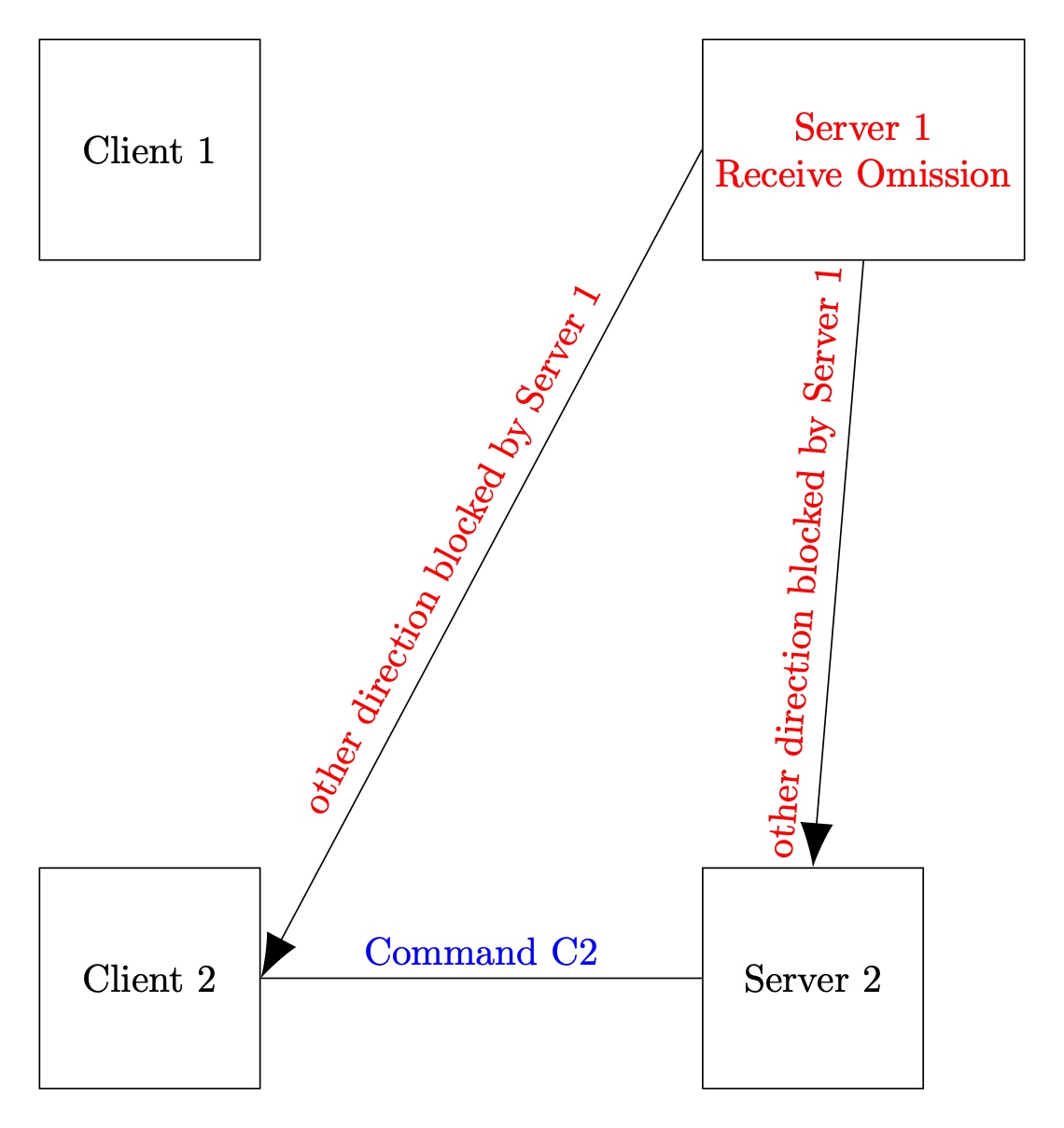
World B: Server 2 has Send Omission failures

Server 2 cannot send any message. Nevertheless, Client 1 and Server 1 must complete the request. Note that Server 2 may learn of this request but cannot convey any outgoing information.

The hybrid world: Server 2 has Send Omission failures and Client 1 has Receive Omission failures

Here we start with Client 2 and Server 2 running an indistinguishable run to World A. Once this completes we let Client 1 and Server 1 run an indistinguishable run to World B.

Note that Server 2 may detect a problem with the second request, but it cannot convey any outgoing information to Client 1 or Server 1.

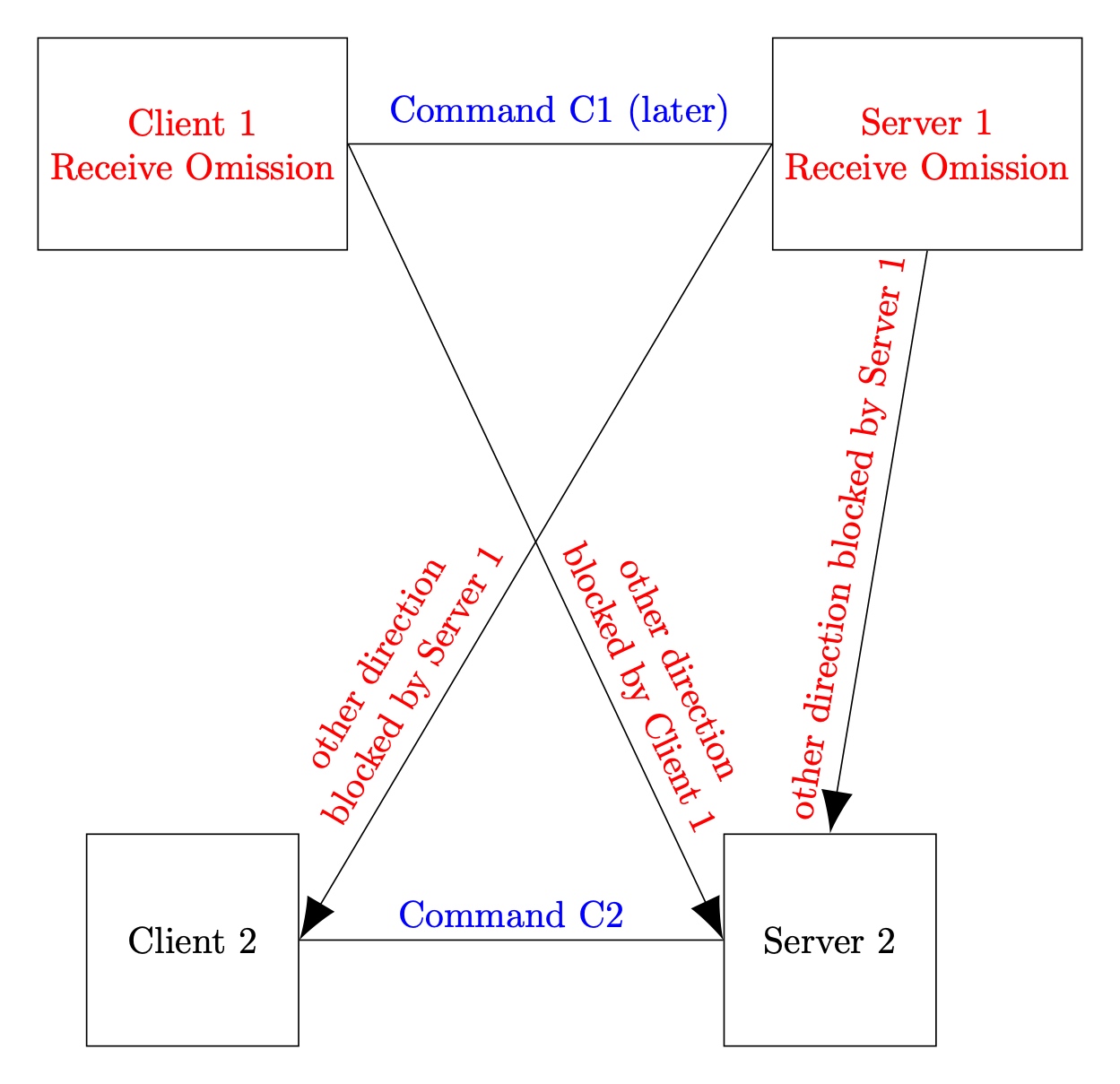
So Client 2 and Server 2 see command 2 and must log it because in world A they would have done so. They then possibly see command 1 as well. Client 1 and Server 1 on the other hand only see command 1 and log it because they would have done so in world B.

This creates a safety violation (assuming there is no validity or liveness violation).

Notes

This lower bound is strictly stronger than the one for omission failures in synchrony.

The upper bounds can be extended to $f<n$ and the lower bound to any $f \geq n/2$.

Acknowledgments

Many thanks to Alon Hovav for noting the lower bound and to Gilad Stern and Kartik Nayak for helpful comments.

Please leave comments on Twitter